Διοικητικές πληροφορίες
| Τίτλος | Παραγωγή και εφαρμογή οπισθοπολλαπλασιασμού |
| Διάρκεια | 60 |
| Ενότητα | Β |
| Είδος μαθήματος | Φροντιστήριο |
| Εστίαση | Τεχνική — Βαθιά Μάθηση |
| Θέμα | Παραγωγή και εφαρμογή της ανατροφοδοτήσεως |
Λέξεις-κλειδιά
Backpropagation, λειτουργίες ενεργοποίησης, απόκλιση,
Μαθησιακοί στόχοι
- Αναπτύξτε μια κατανόηση της διαβάθμισης και του ρυθμού μάθησης
- Αντλεί την οπίσθια αναπαραγωγή για κρυμμένα και εξωτερικά στρώματα
- Οπισθοπολλαπλασιασμός αποσυνδέθηκε και συνδέθηκε χρησιμοποιώντας διαφορετικές λειτουργίες ενεργοποίησης
Αναμενόμενη προετοιμασία
Μαθησιακές εκδηλώσεις που πρέπει να ολοκληρωθούν πριν
Υποχρεωτικό για τους φοιτητές
- Αναθεώρηση του λογισμού (παράγωγα, μερικά παράγωγα, ο κανόνας της αλυσίδας)
Προαιρετικό για Φοιτητές
Καμία.
Αναφορές και υπόβαθρο για τους μαθητές
- John D Kelleher και Brain McNamee. (2018), Fundamentals of Machine Learning for Predictive Data Analytics, MIT Press.
- Ο Μάικλ Νίλσεν. (2015), Neural Networks and Deep Learning (Νευρωνικά δίκτυα και βαθιά μάθηση), 1. Αποφασιστικότητα Τύπος, San Francisco CA ΗΠΑ.
- Charu C. Aggarwal. (2018), Neural Networks and Deep Learning (Νευρωνικά δίκτυα και βαθιά μάθηση), 1. Σπρίνγκερ
- Αντόνιο Γκούλι, Σουτζίτ Παλ. Βαθιά μάθηση με Keras, Packt, [ISBN: 9781787128422].
Συνιστάται για εκπαιδευτικούς
Καμία.
Υλικό μαθήματος
Οδηγίες για τους εκπαιδευτικούς
- Αυτό το σεμινάριο θα εισαγάγει τους μαθητές στις βασικές αρχές του αλγορίθμου μάθησης για ένα τεχνητό νευρωνικό δίκτυο. Αυτό το σεμινάριο θα αποτελείται από την παραγωγή του αλγορίθμου backpropagation χρησιμοποιώντας στυλό και χαρτί, στη συνέχεια την εφαρμογή του αλγορίθμου backpropagation για τρεις διαφορετικές λειτουργίες ενεργοποίησης κρυφού στρώματος (Sigmoid, Tan H και ReLu), χρησιμοποιώντας Python με μόνο τη βιβλιοθήκη Numpy (για χειρισμό πινάκων) και στη συνέχεια χρησιμοποιώντας KERAS. Αυτό θα βασιστεί στη θεμελιώδη κατανόηση των ποικίλων συναρτήσεων ενεργοποίησης όταν ένα νευρωνικό δίκτυο μαθαίνει και πώς οι συναρτήσεις ενεργοποίησης διαφέρουν στην υπολογιστική πολυπλοκότητα και την εφαρμογή από στυλό και χαρτί, σε κώδικα από την αρχή χρησιμοποιώντας Numpy και στη συνέχεια χρησιμοποιώντας μια ενότητα υψηλού επιπέδου -> Keras.
- Σημείωση: Η τοπολογία είναι η ίδια με τη Διάλεξη 1/Tutorial 1, αλλά τα βάρη και οι εισροές είναι διαφορετικές, μπορείτε φυσικά να χρησιμοποιήσετε τα ίδια βάρη.
- Στους μαθητές θα παρουσιαστούν τέσσερα προβλήματα (το πρώτο είναι προαιρετικό ή ως πρόσθετο υλικό):
- Πρόβλημα 1: Η παραγωγή του αλγορίθμου οπισθοπολλαπλασιασμού (χρησιμοποιώντας τη συνάρτηση Sigmoid για τις συναρτήσεις εσωτερικής και εξωτερικής ενεργοποίησης και MSE ως συνάρτηση απώλειας), θα ζητηθεί από τους μαθητές να αντλήσουν τον τύπο οπισθοπολλαπλασιασμού (20 λεπτά για να ολοκληρωθεί).
- Πρόβλημα 2: Οι μαθητές θα εφαρμόσουν τρεις λειτουργίες ενεργοποίησης για μια ενιαία ενημέρωση βάρους (SGD backpropagation), χρησιμοποιώντας στυλό και χαρτί για (20 λεπτά):
- Σιγμοειδές (κρυφό στρώμα), σιγμοειδές (εξωτερική στιβάδα) και MSE
- Tan H (Κρυφό στρώμα), Sigmoid (εξωτερική στρώση) και MSE
- ReLU (Κρυφό στρώμα), Sigmoid (εξωτερική στρώση) και MSE
- Πρόβλημα 3: Οι μαθητές θα κληθούν (με καθοδήγηση ανάλογα με την προηγούμενη εμπειρία κωδικοποίησης) να αναπτύξουν ένα νευρωνικό δίκτυο από την αρχή χρησιμοποιώντας μόνο την ενότητα Numpy, και τα βάρη και τις λειτουργίες ενεργοποίησης όπου παρέχεται η επιλογή από οποιαδήποτε κρυφή λειτουργία ενεργοποίησης στρώματος για να ενημερώσετε τα βάρη χρησιμοποιώντας SGD (20 λεπτά για να ολοκληρωθεί).
- Πρόβλημα 4: Οι μαθητές θα κληθούν (με καθοδήγηση ανάλογα με την προηγούμενη εμπειρία κωδικοποίησης) να αναπτύξουν ένα νευρωνικό δίκτυο χρησιμοποιώντας την ενότητα Tensorflow 2.X με την ενσωματωμένη ενότητα Keras, και τα βάρη και τις λειτουργίες ενεργοποίησης, και στη συνέχεια χρησιμοποιώντας τυχαία βάρη για να ολοκληρώσουν μία ή περισσότερες ενημερώσεις βάρους. Παρακαλούμε όχι επειδή η Keras χρησιμοποιεί μια ελαφρά διαφορετική απώλεια ΠΜΣ, η απώλεια μειώνεται ταχύτερα στο παράδειγμα της Keras.
- Keras MSE = απώλεια = τετράγωνο(y_true — y_pred)
- Φροντιστήριο MSE = απώλεια = (τετράγωνο(y_true — y_pred))*0.5
- Οι υποστόχοι για αυτά τα τρία προβλήματα, είναι να πείσουν τους μαθητές να κατανοήσουν τον αλγόριθμο οπισθοπολλαπλασιασμού, να τον εφαρμόσουν έτσι ώστε για τον συντονισμό των υπερμετρητών, οι μαθητές να είναι σε θέση να κατανοήσουν καλύτερα τα φαινόμενα υπερπαράμετρου.
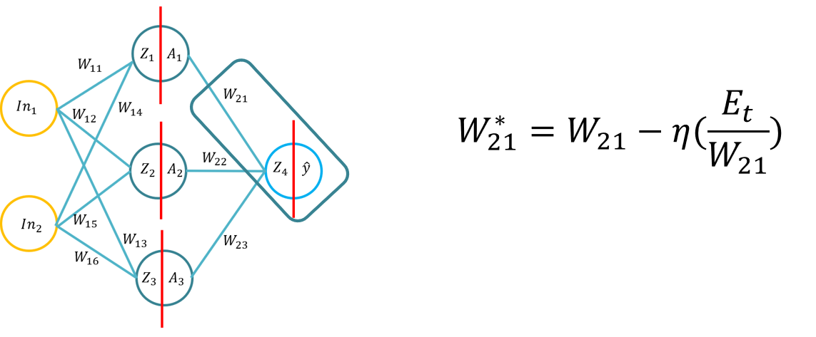
Σχεδιάγραμμα
| Διάρκεια (ελάχιστη) | Περιγραφή |
|---|---|
| 20 (προαιρετικό) | Πρόβλημα 1: παραγωγή του τύπου οπισθοπολλαπλασιασμού χρησιμοποιώντας τη συνάρτηση Sigmoid για τις συναρτήσεις εσωτερικής και εξωτερικής ενεργοποίησης και MSE ως συνάρτηση απώλειας (προαιρετική) |
| 20 | Πρόβλημα 2: Οι μαθητές θα εφαρμόσουν τρεις λειτουργίες ενεργοποίησης για μια ενιαία ενημέρωση βάρους (SGD backpropagation), χρησιμοποιώντας στυλό και χαρτί για (20 λεπτά): |
| 20 | Πρόβλημα 3: Οι μαθητές θα αναπτύξουν ένα νευρωνικό δίκτυο από την αρχή χρησιμοποιώντας μόνο την ενότητα Numpy, όπου ο χρήστης μπορεί να επιλέξει από οποιαδήποτε από τις τρεις κρυμμένες λειτουργίες ενεργοποίησης στρώματος όπου ο κώδικας μπορεί να προδιαμορφώσει την οπίσθια αναπαραγωγή |
| 10 | Πρόβλημα 4: Οι μαθητές θα χρησιμοποιήσουν την ενότητα Tensorflow 2.X με την ενσωματωμένη ενότητα Keras, προδιαμορφωμένη πίσω διάδοση χρησιμοποιώντας SGD. |
| 10 | Ανακεφαλαιοποίηση στη διαδικασία μπροστινής διέλευσης |
Αναγνωρίσεις
Το πρόγραμμα Μάστερ τεχνητής νοημοσύνης με επίκεντρο τον άνθρωπο συγχρηματοδοτήθηκε από τον μηχανισμό «Συνδέοντας την Ευρώπη» της Ευρωπαϊκής Ένωσης στο πλαίσιο της επιχορήγησης CEF-TC-2020-1 Digital Skills 2020-EU-IA-0068.
