Informații administrative
| Titlu | Derivarea și aplicarea backpropagation |
| Durată | 60 |
| Modulul | B |
| Tipul lecției | Tutorial |
| Focalizare | Tehnică – Învățare profundă |
| Subiect | Derivarea și punerea în aplicare a backpropagation |
Cuvinte cheie
Backpropagation, funcții de activare, abatere,
Obiective de învățare
- Dezvoltarea unei înțelegeri a gradientului și a ratei de învățare
- Derivați backpropagation pentru straturile ascunse și exterioare
- Implimentarea Backpropagation deconectată și conectată utilizând diferite funcții de activare
Pregătirea preconizată
Evenimente de învățare care urmează să fie finalizate înainte
Obligatoriu pentru studenți
- Revizuirea calculului (derivative, derivate parțiale, regula lanțului)
Opțional pentru studenți
Nici unul.
Referințe și context pentru studenți
- John D Kelleher și Brain McNamee. (2018), Fundamentals of Machine Learning for Predictive Data Analytics, MIT Press.
- Michael Nielsen. (2015), Neural Networks and Deep Learning (Rețele neuronale și învățare profundă), 1. Presa de determinare, San Francisco CA SUA.
- Charu C. Aggarwal. (2018), Neural Networks and Deep Learning (Rețele neuronale și învățare profundă), 1. Springer
- Antonio Gulli, Sujit Pal. Deep Learning cu Keras, Packt, [ISBN: 9781787128422].
Recomandat pentru profesori
Nici unul.
Materiale de lecție
Instrucțiuni pentru profesori
- Acest tutorial va introduce elevii la fundamentele algoritmului de învățare backpropagation pentru o rețea neuronală artificială. Acest tutorial va consta în derivarea algoritmului backpropagation folosind stiloul și hârtia, apoi aplicarea algoritmului backpropagation pentru trei funcții diferite de activare a stratului ascuns (Sigmoid, Tan H și ReLu), folosind Python doar cu biblioteca Numpy (pentru manipularea matricelor) și apoi folosind KERAS. Acest lucru se va baza pe înțelegerea fundamentală a funcțiilor de activare diferite atunci când o rețea neuronală învață și modul în care funcțiile de activare diferă în complexitatea computațională și aplicația de la stilou și hârtie, la cod de la zero folosind Numpy și apoi folosind un modul de nivel înalt -> Keras.
- Notă: Topologia este aceeași cu Lecture 1/Tutorial 1, dar greutățile și intrările sunt diferite, puteți folosi, desigur, aceleași greutăți.
- Elevilor li se vor prezenta patru probleme (prima fiind opțională sau ca material suplimentar):
- Problema 1: Derivarea algoritmului backpropagation (folosind funcția Sigmoid pentru funcțiile de activare interioară și exterioară și MSE ca funcție de pierdere), elevilor li se va cere să obțină formula de backpropagation (20 de minute pentru a finaliza).
- Problema 2: Elevii vor aplica trei funcții de activare pentru o singură actualizare a greutății (SGD backpropagation), folosind stiloul și hârtia pentru (20 de minute):
- Sigmoid (strat ascuns), sigmoid (stratul exterior) și MSE
- Tan H (strat ascuns), sigmoid (stratul exterior) și MSE
- ReLU (strat ascuns), sigmoid (stratul exterior) și MSE
- Problema 3: Elevii vor fi rugați (cu îndrumare în funcție de experiența anterioară de codificare) să dezvolte o rețea neuronală de la zero folosind numai modulul Numpy, iar greutățile și funcțiile de activare în cazul în care opțiunea de a selecta din orice funcție de activare a unui strat ascuns este furnizată pentru a actualiza greutățile folosind SGD (20 de minute pentru a finaliza).
- Problema 4: Elevii vor fi rugați (cu îndrumare în funcție de experiența de codificare anterioară) să dezvolte o rețea neuronală utilizând modulul Tensorflow 2.X cu modulul inbuild Keras și greutățile și funcțiile de activare și apoi folosind greutăți aleatorii pentru a finaliza una sau mai multe actualizări de greutate. Vă rugăm să nu, deoarece Keras utilizează o ușoară pierdere diferită a MSE, pierderea se reduce mai repede în exemplul Keras.
- Keras MSE = pierdere = pătrat(y_true – y_pred)
- Tutorial MSE = pierdere = [pătrat(y_true – y_pred)]*0.5
- Subscopul acestor trei probleme este de a-i face pe elevi să înțeleagă algoritmul de backpropagation, să-l aplice astfel încât, pentru tuningul hipermetrului, elevii să poată înțelege mai bine efectele hiperparametrului.
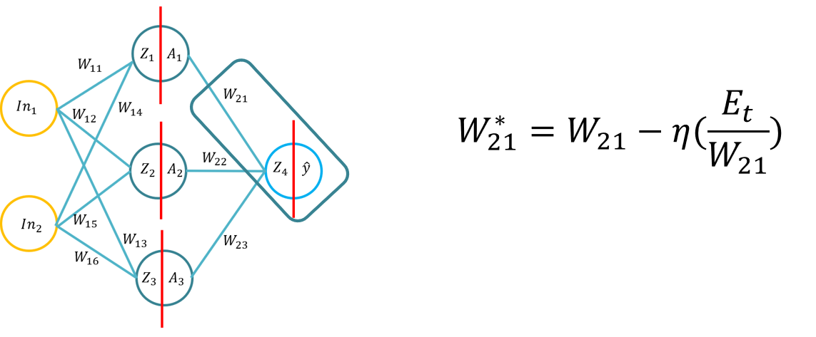
Contur
| Durată (min) | Descriere |
|---|---|
| 20 (opțional) | Problema 1: derivarea formulei de backpropagare utilizând funcția Sigmoid pentru funcțiile de activare interioară și exterioară și MSE ca funcție de pierdere (opțional) |
| 20 | Problema 2: Elevii vor aplica trei funcții de activare pentru o singură actualizare a greutății (SGD backpropagation), folosind stiloul și hârtia pentru (20 de minute): |
| 20 | Problema 3: Elevii vor dezvolta o rețea neuronală de la zero folosind doar modulul Numpy, în cazul în care utilizatorul poate selecta din oricare dintre cele trei funcții de activare strat ascuns în cazul în care codul poate preforma backpropagation |
| 10 | Problema 4: Elevii vor utiliza modulul Tensorflow 2.X cu modulul inbuild Keras, preforma backpropagation folosind SGD. |
| 10 | Recapitularea procesului de trecere înainte |
Confirmări
Programul de masterat AI centrat pe om a fost cofinantat de Mecanismul pentru interconectarea Europei al Uniunii Europene sub Grantul CEF-TC-2020-1 Digital Skills 2020-EU-IA-0068.
